| 1 |

|
(C) |
|
Conceptually, quintupling all forces, and consequently ∆x (including the errors) would leave the error in k the same. So quintupling the values but not the errors multiplies the error in k by 0.2. Quantitatively, we use the equation for relative errors:
�(δk/k)^2=�(δF/F)^2 �+ (δx/∆x)^2
The denominators on the right hand side will quintuple when Tiffany does the measurement, hence, the new uncertainty is 1/5δkS.
|
Conceptually, quintupling all forces, and consequently ∆x (including the errors) would leave the error in k the same. So quintupling the values but not the errors multiplies the error in k by 0.2. Quantitatively, we use the equation for relative errors:
�(δk/k)^2=�(δF/F)^2 �+ (δx/∆x)^2
The denominators on the right hand side will quintuple when Tiffany does the measurement, hence, the new uncertainty is 1/5δkS.
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 2 |

|
(C) |
|
Suppose we call z the height measured from the middle of the box and x the horizontal displacement, also measured from the middle of the box. When the ball is at equilibrium at some z0, the springs obey
−k1z0 − k2z0 = mg.
We can use this to find the equilibrium position,
z0 = −mg/k1 + k2
Imagine a horizontal displacement of size x. If x is small, the tension in the top spring is not changed from the tension at equilibrium (to first order in x). So the restoring force is
F1 = T1 sinθ ≈ T1θ ≈ −k1xz0/l0 − z0
where θ ≈ x is the angle the spring makes with the vertical. l0 −z0
The bottom spring similarly exerts a force
F2 ≈ k2xz0/l0 + z0
pushing the ball away from equilibrium.
For equilibrium to be stable, for positive x, we must have
F1 + F2 < 0
Putting in F1 and F2, we have
−k1xz0/l0 − z0 +k2xz0/l0 + z0 <0
Dividing by x and z0, which we recall is negative,
k1/l0 − z0 < k2/l0 + z0
Plugging in our expression for z0 and rearranging this, we derive
k1 − k2 < mg/l0
|
Suppose we call z the height measured from the middle of the box and x the horizontal displacement, also measured from the middle of the box. When the ball is at equilibrium at some z0, the springs obey
−k1z0 − k2z0 = mg.
We can use this to find the equilibrium position,
z0 = −mg/k1 + k2
Imagine a horizontal displacement of size x. If x is small, the tension in the top spring is not changed from the tension at equilibrium (to first order in x). So the restoring force is
F1 = T1 sinθ ≈ T1θ ≈ −k1xz0/l0 − z0
where θ ≈ x is the angle the spring makes with the vertical. l0 −z0
The bottom spring similarly exerts a force
F2 ≈ k2xz0/l0 + z0
pushing the ball away from equilibrium.
For equilibrium to be stable, for positive x, we must have
F1 + F2 < 0
Putting in F1 and F2, we have
−k1xz0/l0 − z0 +k2xz0/l0 + z0 <0
Dividing by x and z0, which we recall is negative,
k1/l0 − z0 < k2/l0 + z0
Plugging in our expression for z0 and rearranging this, we derive
k1 − k2 < mg/l0
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 3 |
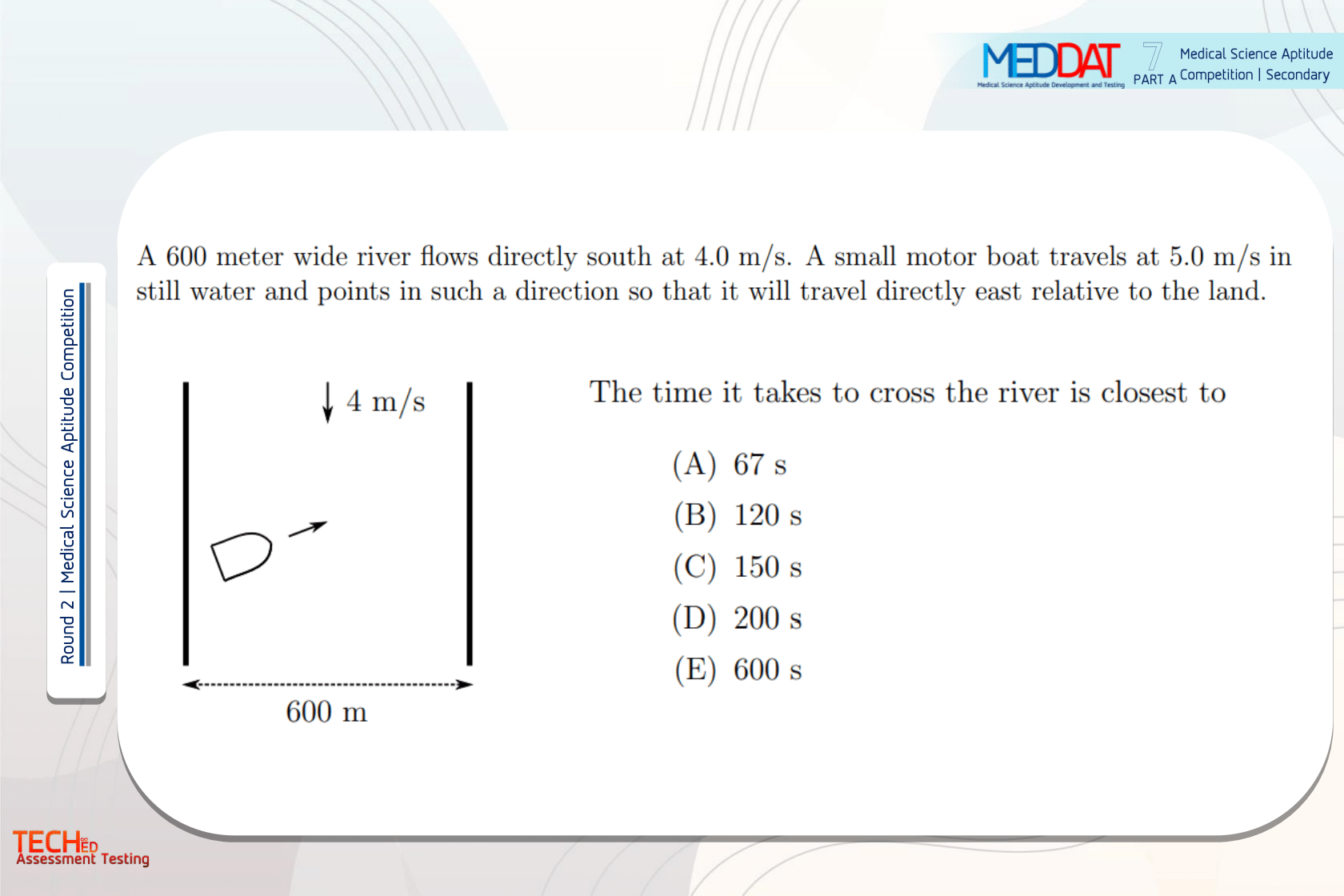
|
(D) |
|
The speed of the boat relative to the land is 3.0 m/s; a vector diagram will illustrate that.
|
600 / 3.0 = 200s
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 4 |

|
(E) |
|
Utilize the numerical values obtained from the preceding inquiry, or employ advanced techniques to compute the desired outcome. The following expression should be considered:
p2f^2 + p1f^2 = p^21i ,
and then
∆K=1/2(p2f^2/m2 + p1f^2/m1 - p^21i/m1) = 1/2(p2f^2/m2 - p2f^2/m1)
so that
∆K= 1/2*p2f^2/m1(m1/m2 - 1)
This is clearly a negative number, and clearly smaller in magnitude than Ki.
|
Utilize the numerical values obtained from the preceding inquiry, or employ advanced techniques to compute the desired outcome. The following expression should be considered:
p2f^2 + p1f^2 = p^21i ,
and then
∆K=1/2(p2f^2/m2 + p1f^2/m1 - p^21i/m1) = 1/2(p2f^2/m2 - p2f^2/m1)
so that
∆K= 1/2*p2f^2/m1(m1/m2 - 1)
This is clearly a negative number, and clearly smaller in magnitude than Ki.
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 5 |
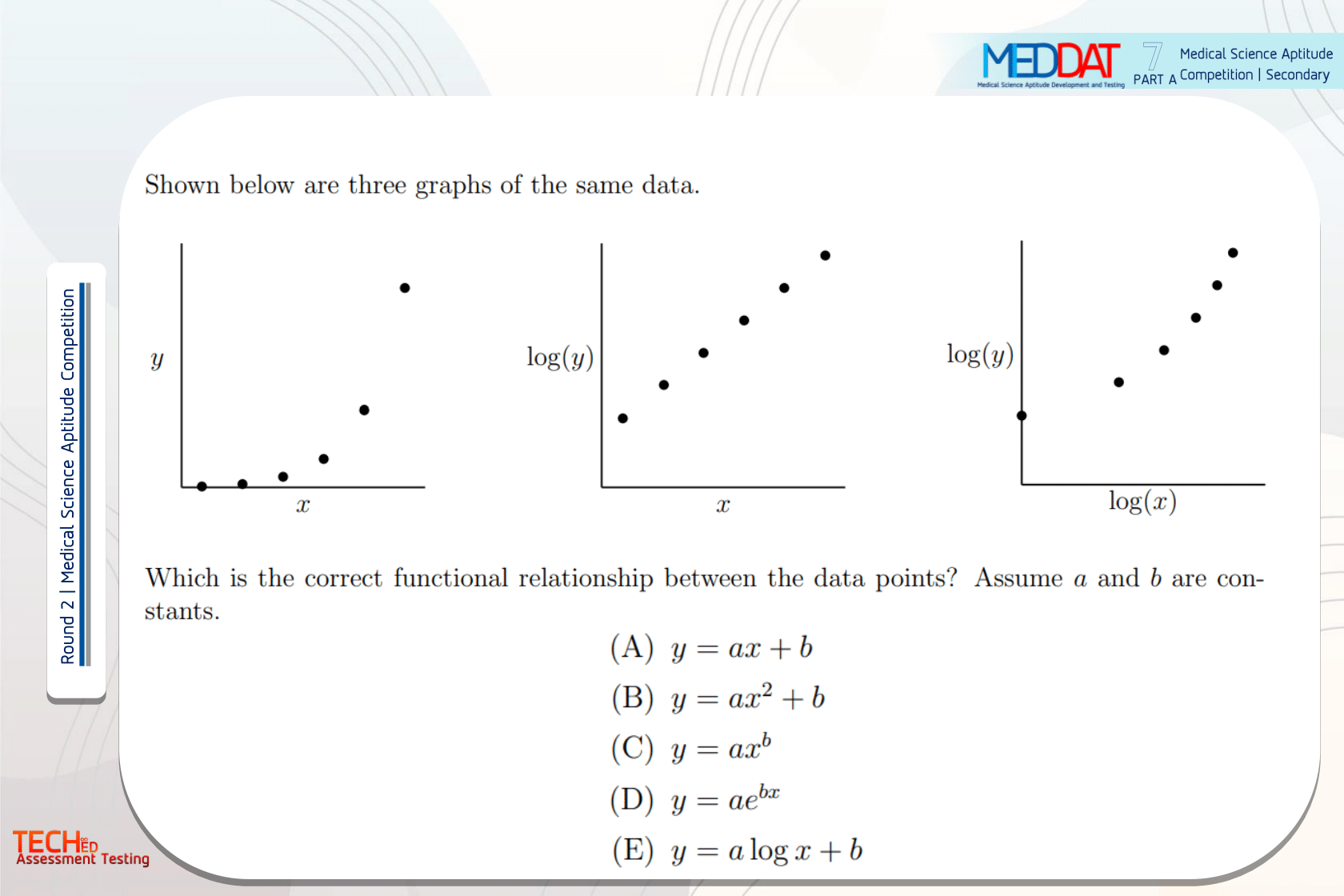
|
(D) |
|
Since the log-linear graph is a straight line, it is the correct functional form:
log y = Ax + B or y = ae^bx
|
Since the log-linear graph is a straight line, it is the correct functional form:
log y = Ax + B or y = ae^bx
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 6 |

|
(A) |
|
The gauge pressure is zero by definition at the top, so it is p1h1g at the liquid interface. The pressure then increases by p2h2g from here to the bottom of the vessel, giving the answer, (p1h1 + p2h2)g.
|
The gauge pressure is zero by definition at the top, so it is p1h1g at the liquid interface. The pressure then increases by p2h2g from here to the bottom of the vessel, giving the answer, (p1h1 + p2h2)g.
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 7 |

|
(D) |
|
The change in surface area, and hence the energy released, is proportional to r^2. The mass is proportional to r^3. Since the energy released is equal to mgh, we have h ∝ r^−1.
|
The change in surface area, and hence the energy released, is proportional to r^2. The mass is proportional to r^3. Since the energy released is equal to mgh, we have h ∝ r^−1.
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 8 |

|
(B) |
|
The force on the scale has three components: (1) Shrek’s weight, (2) the weight of the water collected in the ogre hat, and (3) the pressure associated with changing the momentum of the downward-falling rain. Component (1) gives a constant weight 5000 N. Component (2) is equal to the weight of the water collected in the hat. The total volume of water collected is V = (1 mm/s) *A*t,andtheweightofthewaterisV*(1000kg/m3)*g=10*t.
Component (3) can be found by noting that in a time t, the total mass M = ρV of water that hits the hat has its momentum changed from p = Mv to zero. Here ρ = 1000kg/m^3 is the density of water. The force applied by the hat on the water is therefore F = ∆p/∆t = Mv/t = 1 N.
Adding these three contributions together gives a total weight W = 5000 + 1 + 10t.
|
The force on the scale has three components: (1) Shrek’s weight, (2) the weight of the water collected in the ogre hat, and (3) the pressure associated with changing the momentum of the downward-falling rain. Component (1) gives a constant weight 5000 N. Component (2) is equal to the weight of the water collected in the hat. The total volume of water collected is V = (1 mm/s) *A*t,andtheweightofthewaterisV*(1000kg/m3)*g=10*t.
Component (3) can be found by noting that in a time t, the total mass M = ρV of water that hits the hat has its momentum changed from p = Mv to zero. Here ρ = 1000kg/m^3 is the density of water. The force applied by the hat on the water is therefore F = ∆p/∆t = Mv/t = 1 N.
Adding these three contributions together gives a total weight W = 5000 + 1 + 10t.
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 9 |

|
(E) |
|
Instantaneously, each cylinder can be thought of as rotating about its point of contact with the ground or plate below. The rotational angular velocity is ω. This means that, relative to the bottom of the cylinder, the top is moving at speed 2ωr. So the first plate is moving to the right at 2ωr. The second plate moves to the right at 2ωr faster than the first, and the top plate moves to the right at 6ωr.
|
Instantaneously, each cylinder can be thought of as rotating about its point of contact with the ground or plate below. The rotational angular velocity is ω. This means that, relative to the bottom of the cylinder, the top is moving at speed 2ωr. So the first plate is moving to the right at 2ωr. The second plate moves to the right at 2ωr faster than the first, and the top plate moves to the right at 6ωr.
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 10 |

|
(A) |
|
In a collision, momentum is conserved whether the collision is elastic or inelastic. This means ∆P = 0 regardless of reference frame, so ∆P does not depend on frame.
In an elastic collision, ∆K = 0, which is again independent of frame. In an inelastic collision, whatever kinetic energy is dissipated will go to heat up the masses (assuming they are isolated, and energy can only go into thermal energy). The heat capacity and temperature change of the masses are both frame-invariant, so the kinetic energy dissipated is again independent of reference frame. (This can also be shown more straightforwardly by direct calculation.)
|
In a collision, momentum is conserved whether the collision is elastic or inelastic. This means ∆P = 0 regardless of reference frame, so ∆P does not depend on frame.
In an elastic collision, ∆K = 0, which is again independent of frame. In an inelastic collision, whatever kinetic energy is dissipated will go to heat up the masses (assuming they are isolated, and energy can only go into thermal energy). The heat capacity and temperature change of the masses are both frame-invariant, so the kinetic energy dissipated is again independent of reference frame. (This can also be shown more straightforwardly by direct calculation.)
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 11 |

|
(E) |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 12 |

|
(D) |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 13 |

|
(E) |
|
The computation is most straightforward within the energy framework, where E0 = mgh + 1 mv2/0 = 2Ef = 2mg(2h). The initial velocity can be determined by solving the equation v0 = √6gh.
|
E0 = mgh + 1 mv2/0 = 2Ef = 2mg(2h)
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 14 |
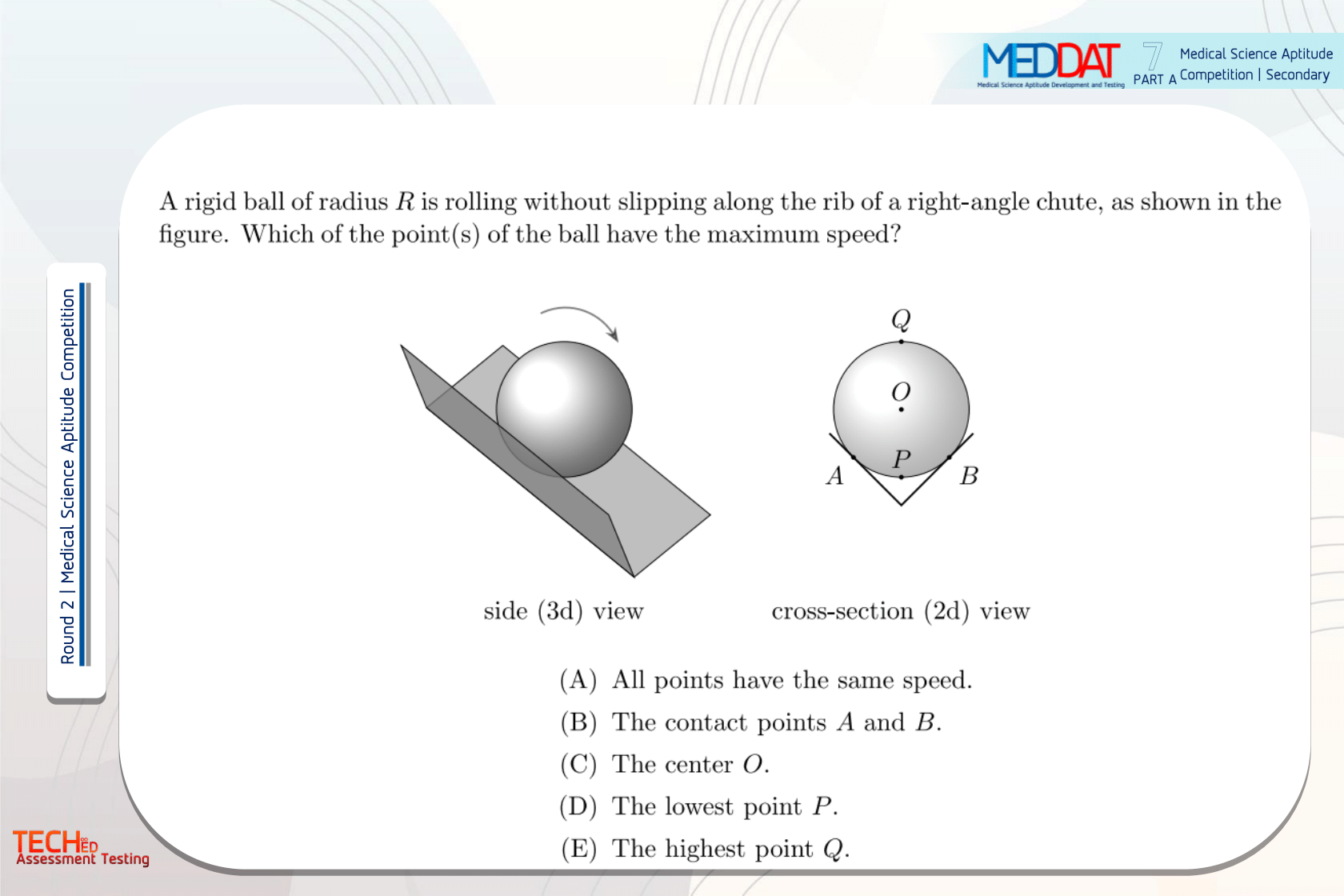
|
(E) |
|
The highest point. In order to maintain the condition of rolling without slipping, it is necessary for objects A and B to remain stationary as they come into contact with the rib. The velocity of a point can be expressed as v + ω × r. Given that the lower part of the ball is stationary, it follows that the highest point of the ball must possess the maximum velocity. It can be demonstrated with clarity that Vtop is equivalent to v(2+root3/root3).
|
Vtop = v(2+root3/root3)
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 15 |

|
(E) |
|
Kepler's third law states that the square of the orbital period (T) of a planet is proportional to the cube of its semimajor axis (a). Additionally, the potential energy (E) of a two-body system can be expressed as negative half of the product of the gravitational constant (G), the mass of one body (M), and the mass of the other body (m), divided by twice the semimajor axis (a). The energy contribution of the astronaut's throw to the overall energy of the trash is deemed insignificant, consequently, it has a negligible effect on the value of a and ultimately on T. Upon completion of a single orbit, it can be observed that the three debris fragments exhibit a cyclical pattern of returning to the space station.
|
By Kepler’s third law, T2 ∝ a3
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 16 |
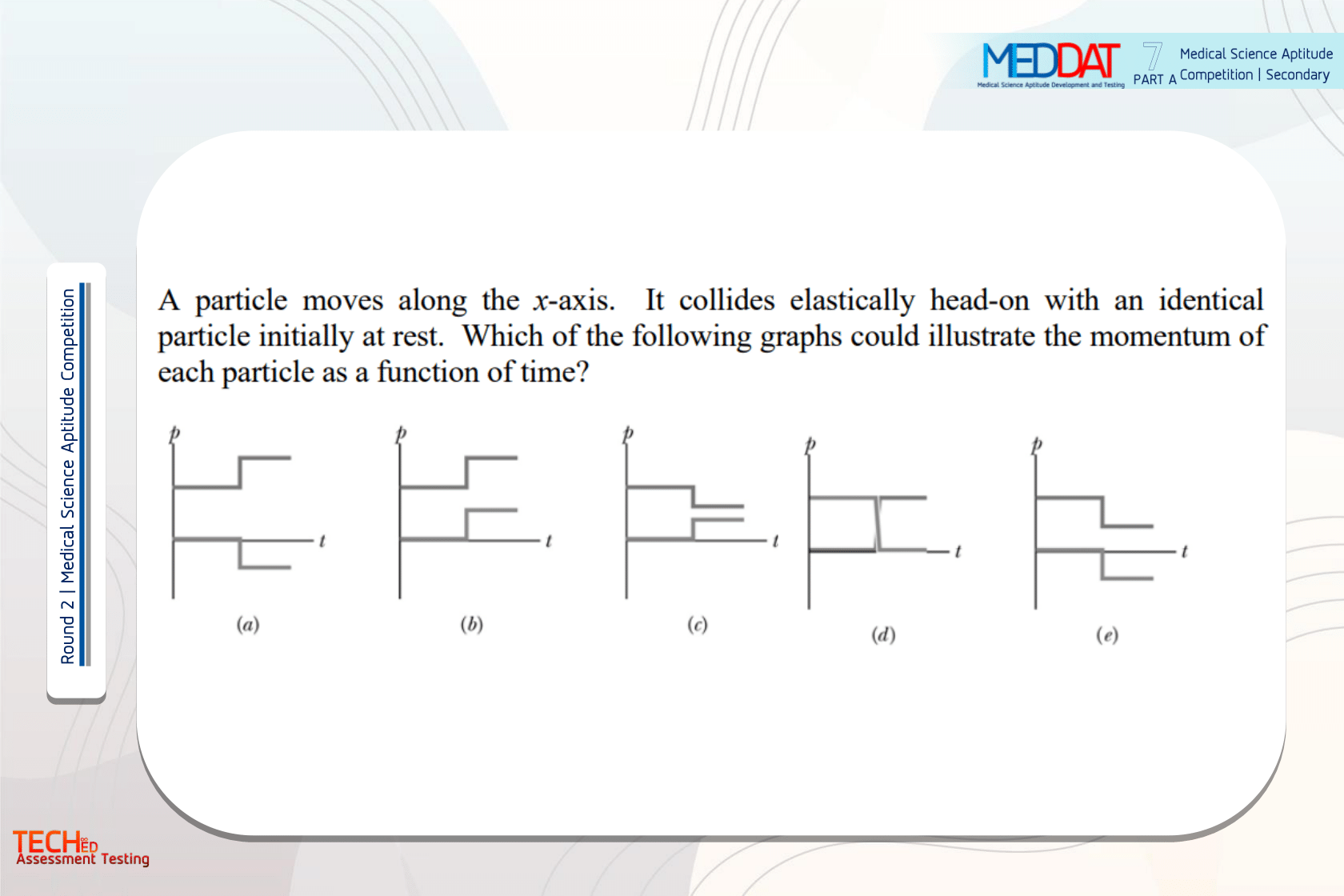
|
(D) |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 17 |

|
(A) |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 18 |

|
(B) |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 19 |

|
(A) |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 20 |

|
(C) |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|