| 1 |
|
2. มีประสิทธิภาพ |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 2 |

|
5. ผิดมากกว่า 1 ข้อ |
|
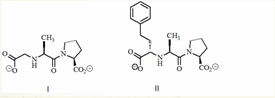
เพราะว่า Ampicillin, Warfarin, Neostigmine, Propranolol นั้นต่างไม่ใช่ลักษณะโมเลกุลแบบExtension แต่โมเลกุลของเป็นส่วนประกอบพื้นฐานของโมเลกุลอินทรีย์ แต่ เพราะว่า Ampicillin, Warfarin, Neostigmine, Propranolol นั้นประกอบด้วยอะตอมคาร์บอน ไฮโดรเจนและอะตอมออกซิเจน ซึ่งไม่มีส่วนต่อขยายที่มีการต่อเติมเพิ่มเข้ามาในโครงสร้าง
|
เพราะว่า Ampicillin, Warfarin, Neostigmine, Propranolol นั้นต่างไม่ใช่ลักษณะโมเลกุลแบบExtension แต่โมเลกุลของเป็นส่วนประกอบพื้นฐานของโมเลกุลอินทรีย์ แต่ เพราะว่า Ampicillin, Warfarin, Neostigmine, Propranolol นั้นประกอบด้วยอะตอมคาร์บอน ไฮโดรเจนและอะตอมออกซิเจน ซึ่งไม่มีส่วนต่อขยายที่มีการต่อเติมเพิ่มเข้ามาในโครงสร้าง
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 3 |
|
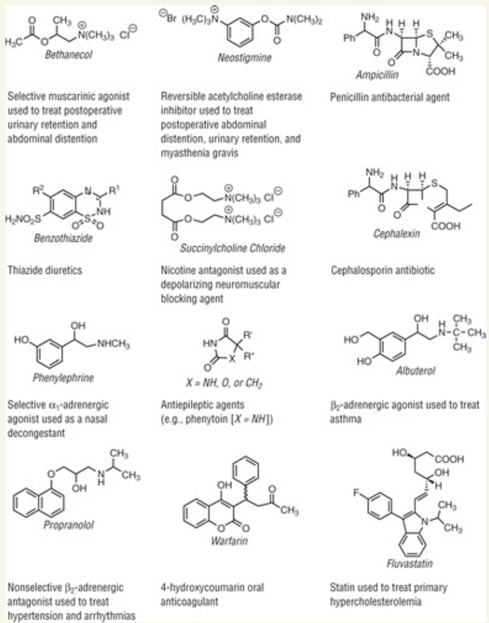
1. Ampicillin |
|
เพราะว่า โมเลกุลของ Ampicillin มีลักษณะเป็นโมเลกุลอินทรีย์ซึ่งประกอบด้วยอะมิโนเป็นหน่วยสร้างสรรค์หลัก มีส่วนประกอบที่สำคัญคือ 6-aminopenicillanic acid (6-APA) ที่เป็นส่วนต่อของโครงสร้างเบต้า-ลัคตัมของยา Ampicillin ส่วนของ Warfarin, Neostigmine, Propranololนั้น เป็นสารประกอบอินทรีย์ที่ประกอบด้วยอะตอมคาร์บอน ฮิโดรเจน และอะตอมไนโตรเจน โดยมีกลุ่มยาสำคัญที่เรียกว่า cholinesterase inhibitors ซึ่งทำหน้าที่เพิ่มการทำงานของสารสื่อประสาทแอซีลโคลีน (acetylcholine) ในระบบประสาท โมเลกุลของ Neostigmine จึงออกฤทธิ์โดยการยับยั้งเอนไซม์คอลีเนสเตอร์เอส (cholinesterases) ซึ่งเป็นเอนไซม์ที่มีบทบาทในการย่อย
|
เพราะว่า โมเลกุลของ Ampicillin มีลักษณะเป็นโมเลกุลอินทรีย์ซึ่งประกอบด้วยอะมิโนเป็นหน่วยสร้างสรรค์หลัก มีส่วนประกอบที่สำคัญคือ 6-aminopenicillanic acid (6-APA) ที่เป็นส่วนต่อของโครงสร้างเบต้า-ลัคตัมของยา Ampicillin ส่วนของ Warfarin, Neostigmine, Propranololนั้น เป็นสารประกอบอินทรีย์ที่ประกอบด้วยอะตอมคาร์บอน ฮิโดรเจน และอะตอมไนโตรเจน โดยมีกลุ่มยาสำคัญที่เรียกว่า cholinesterase inhibitors ซึ่งทำหน้าที่เพิ่มการทำงานของสารสื่อประสาทแอซีลโคลีน (acetylcholine) ในระบบประสาท โมเลกุลของ Neostigmine จึงออกฤทธิ์โดยการยับยั้งเอนไซม์คอลีเนสเตอร์เอส (cholinesterases) ซึ่งเป็นเอนไซม์ที่มีบทบาทในการย่อย
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 4 |
|
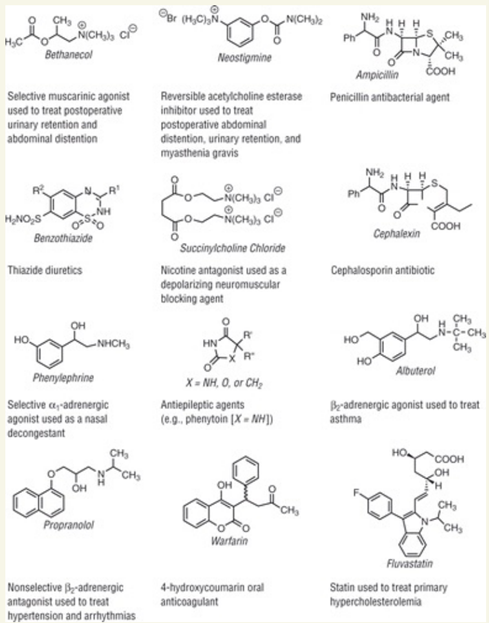
5. มีข้อผิดมากกว่า 1 ข้อ |
|
เพราะว่า Cephalexin เป็นยาปฏิชีวนะแบบสไปโรเทตแบคทีเรีย (cephalosporin) ที่ใช้ในการรักษาการติดเชื้อที่เกี่ยวข้องกับแผลบริเวณผิวหนังและระบบทางเดินหายใจ ส่วน Warfarin ไม่ใช่ยาที่ใช้ในการรักษาโรคเกี่ยวกับปัสสาวะ โมเลกุลของ Warfarin และกลไกการออกฤทธิ์ของยาเน้นไปที่การป้องกันการกลายเป็นลิ่มเลือด โดยยับยั้งการสังเคราะห์และการทำงานของแคล็อตติน (clotting factors) ภายในร่างกาย ส่วน Neostigmine เป็นยาที่ใช้ในการรักษาโรคที่เกี่ยวข้องกับระบบประสาท โดยเฉพาะการรักษากล้ามเนื้อที่อ่อนแรง และ ยา Benzothiazide เป็นยาที่เข้าไปอยู่ในกลุ่มยาไดเออร์ีติก ที่ใช้ในการรักษาโรคความดันโลหิตสูง (hypertension) และปัสสาวะออกมาก (diuresis) โดยการเพิ่มการถ่ายน้ำออกจากร่างกาย การใช้ยา Benzothiazide มักเป็นส่วนหนึ่งของระบบการรักษาโรคความดันโลหิตสูง
|
เพราะว่า Cephalexin เป็นยาปฏิชีวนะแบบสไปโรเทตแบคทีเรีย (cephalosporin) ที่ใช้ในการรักษาการติดเชื้อที่เกี่ยวข้องกับแผลบริเวณผิวหนังและระบบทางเดินหายใจ ส่วน Warfarin ไม่ใช่ยาที่ใช้ในการรักษาโรคเกี่ยวกับปัสสาวะ โมเลกุลของ Warfarin และกลไกการออกฤทธิ์ของยาเน้นไปที่การป้องกันการกลายเป็นลิ่มเลือด โดยยับยั้งการสังเคราะห์และการทำงานของแคล็อตติน (clotting factors) ภายในร่างกาย ส่วน Neostigmine เป็นยาที่ใช้ในการรักษาโรคที่เกี่ยวข้องกับระบบประสาท โดยเฉพาะการรักษากล้ามเนื้อที่อ่อนแรง และ ยา Benzothiazide เป็นยาที่เข้าไปอยู่ในกลุ่มยาไดเออร์ีติก ที่ใช้ในการรักษาโรคความดันโลหิตสูง (hypertension) และปัสสาวะออกมาก (diuresis) โดยการเพิ่มการถ่ายน้ำออกจากร่างกาย การใช้ยา Benzothiazide มักเป็นส่วนหนึ่งของระบบการรักษาโรคความดันโลหิตสูง
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 5 |
การจับยากับตำแหน่งจับของโปรตีน disulfide bond ไม่เกี่ยวข้องกับโรคใด
|
3. stoke |
|
การจับยากับตำแหน่งจับของโปรตีน disulfide bond ยังไม่มีการสังเกตเชื่อมโยงกับโรคหลอดเลือดสมอง (Stroke) โรค Stroke มักเกิดจากปัจจัยหลายอย่าง เช่น การอุดตันหรือแตกของหลอดเลือดสมอง โรคหัวใจ ความดันโลหิตสูง หรือภาวะที่ทำให้เกิดการลิ่มเลือดของหลอดเลือดสมอง การเชื่อมโยงโปรตีนด้วย disulfide bond เป็นกระบวนการที่เกิดภายในโปรตีนเอง และไม่มีความสัมพันธ์โดยตรงกับโรค Stroke อย่างไรก็ตาม การวิจัยต่อไปอาจเป็นประโยชน์ในการศึกษาวิธีการจับยาที่เกี่ยวข้องกับโรค Stroke และกลไกเชื่อมโยงกับโปรตีนในสมอง
|
การจับยากับตำแหน่งจับของโปรตีน disulfide bond ยังไม่มีการสังเกตเชื่อมโยงกับโรคหลอดเลือดสมอง (Stroke) โรค Stroke มักเกิดจากปัจจัยหลายอย่าง เช่น การอุดตันหรือแตกของหลอดเลือดสมอง โรคหัวใจ ความดันโลหิตสูง หรือภาวะที่ทำให้เกิดการลิ่มเลือดของหลอดเลือดสมอง การเชื่อมโยงโปรตีนด้วย disulfide bond เป็นกระบวนการที่เกิดภายในโปรตีนเอง และไม่มีความสัมพันธ์โดยตรงกับโรค Stroke อย่างไรก็ตาม การวิจัยต่อไปอาจเป็นประโยชน์ในการศึกษาวิธีการจับยาที่เกี่ยวข้องกับโรค Stroke และกลไกเชื่อมโยงกับโปรตีนในสมอง
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 6 |
ความเข้มข้นของยาในกระแสเลือดของผู้ป่วยหลังจาก t ชั่วโมง จำลองตามสูตร C (t) = 5(8)^t โดยที่ C วัดเป็นมิลลิกรัมต่อลิตร ความเข้มข้นของยาจะเป็น 80 มิลลิกรัมต่อลิตร ที่กี่ชั่วโมง
|
1. 1.33 |
|
เพื่อหาชั่วโมงที่ความเข้มข้นของยาเป็น 80 มิลลิกรัมต่อลิตร ต้องแก้สมการ C(t) = 80 มิลลิกรัมต่อลิตร เท่ากับ 5(8)^t
ดังนั้นเราต้องแก้สมการดังนี้:
80 = 5(8)^t
เริ่มต้นจากการหารด้วย 5 เพื่อลดสูตร:
16 = (8)^t
หลังจากนั้นเราจะนำค่าโลการของ 8 เท่ากับ 2 เข้าไปในสมการ:
16 = 2^3t
หากเขียนใหม่อีกครั้ง:
2^4 = 2^3t
เพื่อที่จะเปรียบเทียบซ้ายมือและขวามือของสมการ จะได้:
4 = 3t
นั่นคือ:
t = 4/3
ดังนั้น ความเข้มข้นของยาจะเป็น 80 มิลลิกรัมต่อลิตรที่ 4/3 ชั่วโมง ซึ่งเท่ากับ1.33 ชั่วโมง
|
เพื่อหาชั่วโมงที่ความเข้มข้นของยาเป็น 80 มิลลิกรัมต่อลิตร ต้องแก้สมการ C(t) = 80 มิลลิกรัมต่อลิตร เท่ากับ 5(8)^t
ดังนั้นเราต้องแก้สมการดังนี้:
80 = 5(8)^t
เริ่มต้นจากการหารด้วย 5 เพื่อลดสูตร:
16 = (8)^t
หลังจากนั้นเราจะนำค่าโลการของ 8 เท่ากับ 2 เข้าไปในสมการ:
16 = 2^3t
หากเขียนใหม่อีกครั้ง:
2^4 = 2^3t
เพื่อที่จะเปรียบเทียบซ้ายมือและขวามือของสมการ จะได้:
4 = 3t
นั่นคือ:
t = 4/3
ดังนั้น ความเข้มข้นของยาจะเป็น 80 มิลลิกรัมต่อลิตรที่ 4/3 ชั่วโมง ซึ่งเท่ากับ1.33 ชั่วโมง
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 7 |
ข้อใดเกี่ยวข้องกับ plasma measures of GFAP
|
3. CSW levels |
|
CSW Levels หรือ Cerebral Spinal Fluid (CSF) Wetness Levels เป็นตัวชี้วัดทางพลาสมาของ GFAP ซึ่งเป็นสารชี้วัดที่เกี่ยวข้องกับการประเมินความรุนแรงของการเกิดการทำลายของเซลล์เส้นใยกระดูกสมอง (neurodegeneration) หรือความผิดปกติในระบบประสาทส่วนกลาง เมื่อมีการเกิดความเสี่ยงหรือความเสียหายในสมอง เซลล์เส้นใยกระดูกสมองจะปล่อย GFAP เข้าสู่ CSF ซึ่งสามารถวัดระดับ GFAP ใน CSF เพื่อประเมินความรุนแรงของภาวะเหล่านี้ได้
|
CSW Levels หรือ Cerebral Spinal Fluid (CSF) Wetness Levels เป็นตัวชี้วัดทางพลาสมาของ GFAP ซึ่งเป็นสารชี้วัดที่เกี่ยวข้องกับการประเมินความรุนแรงของการเกิดการทำลายของเซลล์เส้นใยกระดูกสมอง (neurodegeneration) หรือความผิดปกติในระบบประสาทส่วนกลาง เมื่อมีการเกิดความเสี่ยงหรือความเสียหายในสมอง เซลล์เส้นใยกระดูกสมองจะปล่อย GFAP เข้าสู่ CSF ซึ่งสามารถวัดระดับ GFAP ใน CSF เพื่อประเมินความรุนแรงของภาวะเหล่านี้ได้
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 8 |
ข้อความใดต่อไปนี้ถูกต้องเกี่ยวกับอันตรกิริยาการจับที่เป็นไปได้ของเอไมด์ทุติยภูมิ
|
2. สามารถเข้าร่วมในพันธะไฮโดรเจนได้ในฐานะตัวรับพันธะไฮโดรเจนเท่านั้น |
|
|
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 9 |
ความเข้มข้นของยาในกระแสเลือดของผู้ป่วยหลังจาก t ชั่วโมง จำลองตามสูตร C (t) = 5(0.5)^t โดยที่ C วัดเป็นมิลลิกรัมต่อลิตร ต้องใช้เวลานานเท่าใดที่ความเข้มข้นจะลดลงถึง 70% ของระดับเริ่มต้น
|
4. 4.8 hr |
|
เราสามารถหาเวลาที่ความเข้มข้นลดลงถึง 70% ของระดับเริ่มต้นได้โดยใช้สูตรที่กำหนดให้:
C(t) = 5(0.5)^t
เมื่อ C(t) คือความเข้มข้นของยาในกระแสเลือดหลังจาก t ชั่วโมง เราต้องหาเวลา t ที่ความเข้มข้นเท่ากับ 70% ของระดับเริ่มต้น (C(0)):
0.7C(0) = 5(0.5)^t
เราสามารถแก้สมการนี้เพื่อหาค่า t ได้:
0.7(5) = (0.5)^t
3.5 = (0.5)^t
เพื่อหาค่า t ที่เป็นไปได้ เราสามารถใช้ log base 0.5 ทั้งสองข้างของสมการ:
log base 0.5 (3.5) = t
t ≈ 4.807
ดังนั้น เวลาที่ความเข้มข้นของยาลดลงถึง 70% ของระดับเริ่มต้นคือประมาณ 4.807 ชั่วโมง
|
เราสามารถหาเวลาที่ความเข้มข้นลดลงถึง 70% ของระดับเริ่มต้นได้โดยใช้สูตรที่กำหนดให้:
C(t) = 5(0.5)^t
เมื่อ C(t) คือความเข้มข้นของยาในกระแสเลือดหลังจาก t ชั่วโมง เราต้องหาเวลา t ที่ความเข้มข้นเท่ากับ 70% ของระดับเริ่มต้น (C(0)):
0.7C(0) = 5(0.5)^t
เราสามารถแก้สมการนี้เพื่อหาค่า t ได้:
0.7(5) = (0.5)^t
3.5 = (0.5)^t
เพื่อหาค่า t ที่เป็นไปได้ เราสามารถใช้ log base 0.5 ทั้งสองข้างของสมการ:
log base 0.5 (3.5) = t
t ≈ 4.807
ดังนั้น เวลาที่ความเข้มข้นของยาลดลงถึง 70% ของระดับเริ่มต้นคือประมาณ 4.807 ชั่วโมง
|
5 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 10 |
ข้อใดมีผลต่อ Aβ-dependent tau phosphorylation
|
1. Astrocyte reactivity |
|
Astrocyte Reactivity (การตอบสนองของเอสโทรไซต์) สามารถมีผลต่อ Aβ-dependent tau phosphorylation (การฟอสโฟริเลชันทาวที่ขึ้นอยู่กับ Aβ) ได้ โดยทั่วไปเรารู้ว่าเอสโทรไซต์เป็นเซลล์เส้นใยกระดูกสมองที่มีบทบาทในการสนับสนุนการทำงานของเองและเอื้อเฟื้อต่อเซลล์เส้นใยและนิวรอนในสมอง
ในบางกรณี เมื่อเกิดการตอบสนองของเอสโทรไซต์ (Astrocyte Reactivity) เช่นเกิดการเรียกคืนเอ็มฟลัสมาตรการฟอสฟาตาว์ (Astrocyte-mediated phagocytosis) หรือการสร้างสารกำลังตัวที่มีต่อ Aβ (Astrocyte-derived factors) อาจส่งผลให้เกิดการลดลงของการฟอสโฟริเลชันทาวที่ขึ้นอยู่กับ Aβ โดยตรง นั่นหมายความว่า Astrocyte Reactivity อาจเป็นส่วนหนึ่งที่มีผลต่อการควบคุมการฟอสโฟริเลชันทาวที่เกี่ยวข้องกับ Aβ ในระบบประสาทส่วนกลาง
|
Astrocyte Reactivity (การตอบสนองของเอสโทรไซต์) สามารถมีผลต่อ Aβ-dependent tau phosphorylation (การฟอสโฟริเลชันทาวที่ขึ้นอยู่กับ Aβ) ได้ โดยทั่วไปเรารู้ว่าเอสโทรไซต์เป็นเซลล์เส้นใยกระดูกสมองที่มีบทบาทในการสนับสนุนการทำงานของเองและเอื้อเฟื้อต่อเซลล์เส้นใยและนิวรอนในสมอง
ในบางกรณี เมื่อเกิดการตอบสนองของเอสโทรไซต์ (Astrocyte Reactivity) เช่นเกิดการเรียกคืนเอ็มฟลัสมาตรการฟอสฟาตาว์ (Astrocyte-mediated phagocytosis) หรือการสร้างสารกำลังตัวที่มีต่อ Aβ (Astrocyte-derived factors) อาจส่งผลให้เกิดการลดลงของการฟอสโฟริเลชันทาวที่ขึ้นอยู่กับ Aβ โดยตรง นั่นหมายความว่า Astrocyte Reactivity อาจเป็นส่วนหนึ่งที่มีผลต่อการควบคุมการฟอสโฟริเลชันทาวที่เกี่ยวข้องกับ Aβ ในระบบประสาทส่วนกลาง
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 11 |
Drug Concentrations
Exponential functions can be used to model the concentration of a drug in a patient’s body. Suppose the concentration of Drug X in a patient’s bloodstream is modeled by,
C (t) = C0 e^(-rt),
ถ้า r = 0.041 /hr
Co = 9 mg/L
t = 7
จากสมการจงหาความเข้มข้นของยา ณ เวลาที่ฉีด
|
3. 0.99 mg/L |
|
ในการหาความเข้มข้นของยา ณ เวลาที่ฉีด เราต้องแทนค่าที่กำหนดลงในสมการสำหรับ C(t):
C(t) = C0 e^(-rt)
โดยที่ C0 เป็นค่าเริ่มต้น ความเข้มข้นของยา ณ เวลาที่ฉีด r คือค่าคงที่อัตราการกำจัด และ t คือเวลาตั้งแต่ฉีด
ในกรณีนี้ เราจะได้รับว่า r = 0.041 /ชม. Co = 9 มก./ลิตร และ t = 7 ชั่วโมง ดังนั้น เราสามารถแทนค่าเหล่านี้และทำให้ง่ายขึ้น:
C(7) = 9 e^(-0.041 x 7)
C(7) = 9 e^(-0.287)
C(7) ≈ 5.07 mg/L
ดังนั้น ความเข้มข้นของยา X ในกระแสเลือดของผู้ป่วย ณ เวลาที่ฉีดจะอยู่ที่ประมาณ 0.9 มก./ลิตร
|
ในการหาความเข้มข้นของยา ณ เวลาที่ฉีด เราต้องแทนค่าที่กำหนดลงในสมการสำหรับ C(t):
C(t) = C0 e^(-rt)
โดยที่ C0 เป็นค่าเริ่มต้น ความเข้มข้นของยา ณ เวลาที่ฉีด r คือค่าคงที่อัตราการกำจัด และ t คือเวลาตั้งแต่ฉีด
ในกรณีนี้ เราจะได้รับว่า r = 0.041 /ชม. Co = 9 มก./ลิตร และ t = 7 ชั่วโมง ดังนั้น เราสามารถแทนค่าเหล่านี้และทำให้ง่ายขึ้น:
C(7) = 9 e^(-0.041 x 7)
C(7) = 9 e^(-0.287)
C(7) ≈ 5.07 mg/L
ดังนั้น ความเข้มข้นของยา X ในกระแสเลือดของผู้ป่วย ณ เวลาที่ฉีดจะอยู่ที่ประมาณ 0.9 มก./ลิตร
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 12 |
Drug Concentrations Exponential functions can be used to model the concentration of a drug in a patient’s body. Suppose the concentration of Drug X in a patient’s bloodstream is modeled by, C (t) = C0 e^(-rt),
จงหาค่า r ถ้า Initial concentration = 10 mg/L
3 mg/L is shown after 9 hours.
|
1. 0.13 |
|
ในการหาค่าของ r ในฟังก์ชันเอกซ์โปเนนเชียล C(t) = C0 e^(-rt) เราสามารถใช้ข้อมูลที่กำหนดให้ได้
ที่ให้ไว้:
ความเข้มข้นเริ่มต้น (C0) = 10 มก./ลิตร
ความเข้มข้นหลังจาก 9 ชั่วโมง (C(9)) = 3 มก./ลิตร
แทนค่าเหล่านี้ลงในสมการ จะได้:
C(9) = C0 จ^(-9r) = 3
หารทั้งสองข้างของสมการด้วย C0 เราจะได้:
จ^(-9r) = 3/10
ในการแยกเทอมเอกซ์โปเนนเชียล เราจะใช้ลอการิทึมธรรมชาติ (ln) ของทั้งสองข้าง:
ln(e^(-9r)) = ln(3/10)
ลอการิทึมธรรมชาติและฟังก์ชันเอกซ์โปเนนเชียลเป็นการดำเนินการแบบผกผัน ดังนั้นจึงหักล้างกัน:
-9r = ln(3/10)
สุดท้าย เราสามารถแก้หาค่า r ได้โดยการหารทั้งสองข้างด้วย -9:
r = -ln(3/10) / 9
r=0.133775
|
ในการหาค่าของ r ในฟังก์ชันเอกซ์โปเนนเชียล C(t) = C0 e^(-rt) เราสามารถใช้ข้อมูลที่กำหนดให้ได้
ที่ให้ไว้:
ความเข้มข้นเริ่มต้น (C0) = 10 มก./ลิตร
ความเข้มข้นหลังจาก 9 ชั่วโมง (C(9)) = 3 มก./ลิตร
แทนค่าเหล่านี้ลงในสมการ จะได้:
C(9) = C0 จ^(-9r) = 3
หารทั้งสองข้างของสมการด้วย C0 เราจะได้:
จ^(-9r) = 3/10
ในการแยกเทอมเอกซ์โปเนนเชียล เราจะใช้ลอการิทึมธรรมชาติ (ln) ของทั้งสองข้าง:
ln(e^(-9r)) = ln(3/10)
ลอการิทึมธรรมชาติและฟังก์ชันเอกซ์โปเนนเชียลเป็นการดำเนินการแบบผกผัน ดังนั้นจึงหักล้างกัน:
-9r = ln(3/10)
สุดท้าย เราสามารถแก้หาค่า r ได้โดยการหารทั้งสองข้างด้วย -9:
r = -ln(3/10) / 9
r=0.133775
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 13 |
Drug Concentrations
Exponential functions can be used to model the concentration of a drug in a patient’s body. Suppose the concentration of Drug X in a patient’s bloodstream is modeled by,
C (t) = Co e^(-rt),
จงหาสมการที่เป็นไปได้ หากยา x, มี r =0. 09 แล้วมีความเข้มข้นลดลง 80% จาก the model, C(t) = Co e^(-rt)
|
3. In 0.8 = -0.09t |
|
หากต้องการหาสมการที่เป็นไปได้เมื่อค่า r = 0.09 และความเข้มข้นลดลง 80% จากสมการ C(t) = Co e^(-rt) ให้เราหาค่า C0 ที่สอดคล้องกับเงื่อนไขดังกล่าว
ในสมการ C(t) = Co e^(-rt) เมื่อ t = 0 (เวลาเริ่มต้น) ค่า C(t) คือความเข้มข้นเริ่มต้น (C0)
ตามเงื่อนไขที่ให้มาว่าความเข้มข้นลดลง 80%
ดังนั้นเราสามารถเขียนสมการใหม่ได้ว่า:
0.8C0 = C0 e^(-0.09t)
สามารถลดส่วน C0 ที่อยู่ทั้งสองข้างของสมการออกได้เพื่อให้เหลือเพียงเท่ากัน:
0.8 = e^(-0.09t)
เราสามารถหาค่า t ที่สอดคล้องกับสมการข้างต้นได้โดยใช้การเข้ารหัสธรรมดา (logarithm) โดยเราจะใช้ฟังก์ชัน natural logarithm (ln) เนื่องจากมีความสัมพันธ์กับฟังก์ชัน exponential:
ln(0.8) = -0.09t
หลังจากนั้นเราสามารถแก้สมการเพื่อหาค่า t ได้:
t = ln(0.8) / (-0.09)
ในกรณีนี้เราใช้ล็อกนาทรัพย์ธรรมดาเนื่องจากเราต้องการหาเวลา (t) ที่เป็นเลขบวก
อย่างไรก็ตามเมื่อคำนวณด้วยเครื่องคิดเลข ค่า t จะเป็นค่าบวกที่อยู่ระหว่าง 2-3 ชั่วโมง (approximately)
|
หากต้องการหาสมการที่เป็นไปได้เมื่อค่า r = 0.09 และความเข้มข้นลดลง 80% จากสมการ C(t) = Co e^(-rt) ให้เราหาค่า C0 ที่สอดคล้องกับเงื่อนไขดังกล่าว
ในสมการ C(t) = Co e^(-rt) เมื่อ t = 0 (เวลาเริ่มต้น) ค่า C(t) คือความเข้มข้นเริ่มต้น (C0)
ตามเงื่อนไขที่ให้มาว่าความเข้มข้นลดลง 80%
ดังนั้นเราสามารถเขียนสมการใหม่ได้ว่า:
0.8C0 = C0 e^(-0.09t)
สามารถลดส่วน C0 ที่อยู่ทั้งสองข้างของสมการออกได้เพื่อให้เหลือเพียงเท่ากัน:
0.8 = e^(-0.09t)
เราสามารถหาค่า t ที่สอดคล้องกับสมการข้างต้นได้โดยใช้การเข้ารหัสธรรมดา (logarithm) โดยเราจะใช้ฟังก์ชัน natural logarithm (ln) เนื่องจากมีความสัมพันธ์กับฟังก์ชัน exponential:
ln(0.8) = -0.09t
หลังจากนั้นเราสามารถแก้สมการเพื่อหาค่า t ได้:
t = ln(0.8) / (-0.09)
ในกรณีนี้เราใช้ล็อกนาทรัพย์ธรรมดาเนื่องจากเราต้องการหาเวลา (t) ที่เป็นเลขบวก
อย่างไรก็ตามเมื่อคำนวณด้วยเครื่องคิดเลข ค่า t จะเป็นค่าบวกที่อยู่ระหว่าง 2-3 ชั่วโมง (approximately)
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 14 |
การกลายพันธุ์ของยีนใดที่อาจส่งผลต่อระดับ Warfarin
|
5. ไม่มีข้อถูก |
|
ไม่มีคำตอบเพราะ มียีน CYP2C9: ยีนนี้เข้ามาเกี่ยวข้องกับการตั้งค่าเอนไซม์ที่ช่วยย่อยยา Warfarin ในร่างกาย การเป็นแบบตั้งค่าน้อยหรือความผิดปกติของยีนนี้อาจทำให้ยา Warfarin มีประสิทธิภาพสูงกว่าปกติ ซึ่งอาจเป็นอันตรายหรือทำให้ และ ยีน VKORC1: ยีนนี้มีความสัมพันธ์กับเอนไซม์ VKORC1 ที่เกี่ยวข้องกับการสังเคราะห์และกระตุ้นการทำงานของโปรตีน VKORC1 ซึ่งเป็นตัวกำหนดการทำงานของยา Warfarin ในร่างกาย การมีการเปลี่ยนแปลงที่สามารถกระตุ้นได้จากยีน VKORC1 อาจส่งผลให้ยา Warfarin มีประสิทธิภาพมากขึ้นหรือน้อยลง ซึ่งอาจจะต้องปรับขนาดยาให้เหมาะสมเพื่อควบคุมระดับยาในร่างกายได้อย่างถูกต้อง
|
ไม่มีคำตอบเพราะ มียีน CYP2C9: ยีนนี้เข้ามาเกี่ยวข้องกับการตั้งค่าเอนไซม์ที่ช่วยย่อยยา Warfarin ในร่างกาย การเป็นแบบตั้งค่าน้อยหรือความผิดปกติของยีนนี้อาจทำให้ยา Warfarin มีประสิทธิภาพสูงกว่าปกติ ซึ่งอาจเป็นอันตรายหรือทำให้ และ ยีน VKORC1: ยีนนี้มีความสัมพันธ์กับเอนไซม์ VKORC1 ที่เกี่ยวข้องกับการสังเคราะห์และกระตุ้นการทำงานของโปรตีน VKORC1 ซึ่งเป็นตัวกำหนดการทำงานของยา Warfarin ในร่างกาย การมีการเปลี่ยนแปลงที่สามารถกระตุ้นได้จากยีน VKORC1 อาจส่งผลให้ยา Warfarin มีประสิทธิภาพมากขึ้นหรือน้อยลง ซึ่งอาจจะต้องปรับขนาดยาให้เหมาะสมเพื่อควบคุมระดับยาในร่างกายได้อย่างถูกต้อง
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 15 |
เป็นเรื่องปกติที่จะให้ยา Warfarin ในขนาดเริ่มต้นที่แตกต่างกันกับผู้คนตามเชื้อชาติของพวกเขา หากให้น้อยเกินไปจะเกิดอะไรขึ้น
|
5. ไม่มีข้อถูก |
|
เพราะว่า หากให้ยา Warfarin ในขนาดที่น้อยเกินไปหรือไม่เพียงพอสำหรับร่างกายของผู้รับยา อาจเกิดผลข้างเคียงอันตรายได้ เช่น การเกิดเลือดออกอุดตัน (bleeding) ซึ่งอาจเกิดเหตุจากยา Warfarin ที่มีประสิทธิภาพสูงเกินไปในการยับยั้งการเกิดและการทำงานของตัวสังเคราะห์โปรตีนที่เกี่ยวข้องกับการเกิดเลือด (การกระตุ้นและการทำงานของ VKORC1)
|
เพราะว่า หากให้ยา Warfarin ในขนาดที่น้อยเกินไปหรือไม่เพียงพอสำหรับร่างกายของผู้รับยา อาจเกิดผลข้างเคียงอันตรายได้ เช่น การเกิดเลือดออกอุดตัน (bleeding) ซึ่งอาจเกิดเหตุจากยา Warfarin ที่มีประสิทธิภาพสูงเกินไปในการยับยั้งการเกิดและการทำงานของตัวสังเคราะห์โปรตีนที่เกี่ยวข้องกับการเกิดเลือด (การกระตุ้นและการทำงานของ VKORC1)
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 16 |
ข้อใดไม่ใช่กลไกการออกฤทธิ์ของ Gleevac
|
4. ผิดทุกข้อ |
|
Gleevac (Imatinib) เป็นยาที่ใช้ในการรักษามะเร็งเม็ดเลือดขาวเรื้อรัง (Chronic Myeloid Leukemia, CML) โดยมีกลไกการออกฤทธิ์ดังนี้:
1. การยับยั้งเอนไซน์ BCR-ABL: Gleevac ทำงานโดยการยับยั้งกิจกรรมของเอนไซน์ BCR-ABL ที่เกี่ยวข้องกับการเกิด CML โดย BCR-ABL เป็นยีนผสมที่เกิดขึ้นจากการย่อยสลายของยีน BCR และยีน ABL ซึ่งเป็นส่วนหนึ่งของเอนไซม์ที่ก่อให้เกิดเซลล์มะเร็งใน CML
2. การยับยั้งกิจกรรมเอนไซน์อื่น: Gleevac อาจยับยั้งกิจกรรมของเอนไซน์อื่นๆ ที่เกี่ยวข้องกับการเกิดและการเจริญของเซลล์มะเร็ง เช่น PDGFR (Platelet-Derived Growth Factor Receptor) และ c-KIT (Receptor Tyrosine Kinase)
3. การยับยั้งการเจริญเติบโตของเซลล์มะเร็ง: Gleevac สามารถยับยั้งกระบวนการเจริญเติบโตของเซลล์มะเร็งได้โดยลดการเจริญเติบโตและการแบ่งเซลล์ของเซลล์มะเร็ง
ดังนั้น กลไกการออกฤทธิ์ของ Gleevac ไม่ได้รวมถึงการกระตุ้นการตายของเซลล์มะเร็ง (apoptosis) ซึ่งเป็นกลไกสำคัญในการรักษามะเร็งในยาบางชนิด
|
Gleevac (Imatinib) เป็นยาที่ใช้ในการรักษามะเร็งเม็ดเลือดขาวเรื้อรัง (Chronic Myeloid Leukemia, CML) โดยมีกลไกการออกฤทธิ์ดังนี้:
1. การยับยั้งเอนไซน์ BCR-ABL: Gleevac ทำงานโดยการยับยั้งกิจกรรมของเอนไซน์ BCR-ABL ที่เกี่ยวข้องกับการเกิด CML โดย BCR-ABL เป็นยีนผสมที่เกิดขึ้นจากการย่อยสลายของยีน BCR และยีน ABL ซึ่งเป็นส่วนหนึ่งของเอนไซม์ที่ก่อให้เกิดเซลล์มะเร็งใน CML
2. การยับยั้งกิจกรรมเอนไซน์อื่น: Gleevac อาจยับยั้งกิจกรรมของเอนไซน์อื่นๆ ที่เกี่ยวข้องกับการเกิดและการเจริญของเซลล์มะเร็ง เช่น PDGFR (Platelet-Derived Growth Factor Receptor) และ c-KIT (Receptor Tyrosine Kinase)
3. การยับยั้งการเจริญเติบโตของเซลล์มะเร็ง: Gleevac สามารถยับยั้งกระบวนการเจริญเติบโตของเซลล์มะเร็งได้โดยลดการเจริญเติบโตและการแบ่งเซลล์ของเซลล์มะเร็ง
ดังนั้น กลไกการออกฤทธิ์ของ Gleevac ไม่ได้รวมถึงการกระตุ้นการตายของเซลล์มะเร็ง (apoptosis) ซึ่งเป็นกลไกสำคัญในการรักษามะเร็งในยาบางชนิด
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 17 |
ข้อใดไม่เกี่ยวข้องกับการขาดกลูโคส -6- ฟอสเฟต G6PD?
|
4. ความเครียด |
|
การขาดกลูโคส-6-ฟอสเฟต G6PD ไม่เกี่ยวข้องโดยตรงกับความเครียด โรค G6PD จะเกิดจากความผิดปกติในเอนไซม์ G6PD ซึ่งเป็นสภาวะทางพันธุกรรม และส่วนใหญ่เกิดขึ้นเมื่อมีการสัมผัสกับสารเคมีที่เกิดขึ้นในอาหาร ยา หรือสารอื่น ๆ ที่สามารถทำให้เกิดการทำลายเซลล์เม็ดเลือดแดงที่มีการขาดกลูโคส-6-ฟอสเฟต G6PD ได้
อย่างไรก็ตาม การเป็นโรค G6PD อาจทำให้ร่างกายมีการตอบสนองที่แตกต่างกับสารเคมีบางชนิดได้ ซึ่งอาจสร้างความเครียดในบางกรณี เช่น เมื่อมีการสัมผัสกับสารที่เป็นตัวกำเนิดสารออกซิเดชัน (oxidative stress) ซึ่งสามารถทำให้เกิดการทำลายเซลล์เม็ดเลือดแดงเพิ่มขึ้น อาจเกิดอาการเบาหวานมีส่วนเกี่ยวข้องกับ G6PD อย่างไรก็ตาม ความเครียดเองไม่ใช่สาเหตุโดยตรงของการขาดกลูโคส-6-ฟอสเฟต G6PD
|
การขาดกลูโคส-6-ฟอสเฟต G6PD ไม่เกี่ยวข้องโดยตรงกับความเครียด โรค G6PD จะเกิดจากความผิดปกติในเอนไซม์ G6PD ซึ่งเป็นสภาวะทางพันธุกรรม และส่วนใหญ่เกิดขึ้นเมื่อมีการสัมผัสกับสารเคมีที่เกิดขึ้นในอาหาร ยา หรือสารอื่น ๆ ที่สามารถทำให้เกิดการทำลายเซลล์เม็ดเลือดแดงที่มีการขาดกลูโคส-6-ฟอสเฟต G6PD ได้
อย่างไรก็ตาม การเป็นโรค G6PD อาจทำให้ร่างกายมีการตอบสนองที่แตกต่างกับสารเคมีบางชนิดได้ ซึ่งอาจสร้างความเครียดในบางกรณี เช่น เมื่อมีการสัมผัสกับสารที่เป็นตัวกำเนิดสารออกซิเดชัน (oxidative stress) ซึ่งสามารถทำให้เกิดการทำลายเซลล์เม็ดเลือดแดงเพิ่มขึ้น อาจเกิดอาการเบาหวานมีส่วนเกี่ยวข้องกับ G6PD อย่างไรก็ตาม ความเครียดเองไม่ใช่สาเหตุโดยตรงของการขาดกลูโคส-6-ฟอสเฟต G6PD
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 18 |
ข้อใดไม่ได้อธิบายสมมติฐาน Life on the Edge ที่เกี่ยวข้องกับโรคอะไมลอยด์
|
5. ผิดทุกข้อ |
|
สมมติฐาน Life on the Edge ที่เกี่ยวข้องกับโรคอะไมลอยด์คือการสมมติว่าอะไมลอยด์อาจมีความเกี่ยวข้องกับการทำงานของระบบประสาทและเซลล์ที่มีอยู่บนขอบเขตระหว่างสถานะสมดุลและสถานะที่เสี่ยง นั่นหมายความว่าอะไมลอยด์อาจเกิดจากการขาดสมดุลของกระบวนการชีวภาพในระดับเซลล์ โดยการศึกษาและทดลองในแง่ของสมมติฐานนี้อาจช่วยให้เราเข้าใจขั้นตอนและเหตุการณ์ที่เกี่ยวข้องกับอะไมลอยด์ได้มากขึ้น อย่างไรก็ตาม สมมติฐานนี้ยังต้องการการวิจัยและการศึกษาเพิ่มเติมเพื่อยืนยันความถูกต้องและความสอดคล้องกับฐานทฤษฎีและหลักการทางวิทยาศาสตร์อย่างเป็นทางการ
|
สมมติฐาน Life on the Edge ที่เกี่ยวข้องกับโรคอะไมลอยด์คือการสมมติว่าอะไมลอยด์อาจมีความเกี่ยวข้องกับการทำงานของระบบประสาทและเซลล์ที่มีอยู่บนขอบเขตระหว่างสถานะสมดุลและสถานะที่เสี่ยง นั่นหมายความว่าอะไมลอยด์อาจเกิดจากการขาดสมดุลของกระบวนการชีวภาพในระดับเซลล์ โดยการศึกษาและทดลองในแง่ของสมมติฐานนี้อาจช่วยให้เราเข้าใจขั้นตอนและเหตุการณ์ที่เกี่ยวข้องกับอะไมลอยด์ได้มากขึ้น อย่างไรก็ตาม สมมติฐานนี้ยังต้องการการวิจัยและการศึกษาเพิ่มเติมเพื่อยืนยันความถูกต้องและความสอดคล้องกับฐานทฤษฎีและหลักการทางวิทยาศาสตร์อย่างเป็นทางการ
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 19 |
ข้อใดเกี่ยวข้องกับ Environmental toxicology
|
5. ถูกมากกว่า 1 ข้อ |
|
เพราะว่า สารเคมี Dichlorodiphenyltrichloroethane (DDT) เป็นสารฆ่าแมลงที่ใช้ในอดีตเพื่อควบคุมแมลงศัตรูพืช อย่างไรก็ตาม DDT เป็นสารพิษที่มีผลกระทบต่อสิ่งแวดล้อมและมีความเกี่ยวข้องกับ Environmental toxicology อย่างมาก การใช้ DDT ในอดีตได้มีผลกระทบต่อสิ่งมีชีวิตในท้องทะเลและแหล่งน้ำจืด โดยเฉพาะสิ่งมีชีวิตในโซนน้ำจืดที่เป็นสัตว์น้ำ นอกจากนี้ DDT ยังสะสมในสิ่งมีชีวิตและสามารถกระจายไปยังสิ่งแวดล้อมทางอากาศและน้ำได้ การสะสมของ DDT ในสิ่งมีชีวิตและสิ่งแวดล้อมอาจมีผลกระทบต่อภาวะสุขภาพและระบบนิเวศ ซึ่งจะต้องมีการศึกษาและการตรวจสอบในสาขา Environmental toxicology เพื่อประเมินผลกระทบของ DDT ต่อสิ่งแวดล้อมและมนุษย์ และ อุตสาหกรรมเคมีผลิตสารเคมีต่าง ๆ มีความเกี่ยวข้องกับ Environmental toxicology (สิ่งเขียวชาววิทยาศาสตร์ในด้านสิ่งแวดล้อม) อย่างมากเนื่องจากสารเคมีที่ถูกใช้ในอุตสาหกรรมบางชนิดอาจมีคุณสมบัติพิษต่อสิ่งแวดล้อมและมนุษย์ เมื่อสารเคมีเข้าสู่สิ่งแวดล้อม เช่น ละอองจากการปล่อยเป็นอากาศหรือน้ำเสียจากโรงงาน หรือการจัดเก็บน้ำเสียที่มีสารเคมี สารเคมีเหล่านี้อาจมีผลกระทบต่อระบบนิเวศและสิ่งมีชีวิต ซึ่งสามารถทำให้เกิดการเปลี่ยนแปลงที่ไม่พึงประสงค์ในสิ่งแวดล้อม ซึ่ง2อย่างนี้มีความเกี่ยวข้องกับ Environmental toxicology
|
เพราะว่า สารเคมี Dichlorodiphenyltrichloroethane (DDT) เป็นสารฆ่าแมลงที่ใช้ในอดีตเพื่อควบคุมแมลงศัตรูพืช อย่างไรก็ตาม DDT เป็นสารพิษที่มีผลกระทบต่อสิ่งแวดล้อมและมีความเกี่ยวข้องกับ Environmental toxicology อย่างมาก การใช้ DDT ในอดีตได้มีผลกระทบต่อสิ่งมีชีวิตในท้องทะเลและแหล่งน้ำจืด โดยเฉพาะสิ่งมีชีวิตในโซนน้ำจืดที่เป็นสัตว์น้ำ นอกจากนี้ DDT ยังสะสมในสิ่งมีชีวิตและสามารถกระจายไปยังสิ่งแวดล้อมทางอากาศและน้ำได้ การสะสมของ DDT ในสิ่งมีชีวิตและสิ่งแวดล้อมอาจมีผลกระทบต่อภาวะสุขภาพและระบบนิเวศ ซึ่งจะต้องมีการศึกษาและการตรวจสอบในสาขา Environmental toxicology เพื่อประเมินผลกระทบของ DDT ต่อสิ่งแวดล้อมและมนุษย์ และ อุตสาหกรรมเคมีผลิตสารเคมีต่าง ๆ มีความเกี่ยวข้องกับ Environmental toxicology (สิ่งเขียวชาววิทยาศาสตร์ในด้านสิ่งแวดล้อม) อย่างมากเนื่องจากสารเคมีที่ถูกใช้ในอุตสาหกรรมบางชนิดอาจมีคุณสมบัติพิษต่อสิ่งแวดล้อมและมนุษย์ เมื่อสารเคมีเข้าสู่สิ่งแวดล้อม เช่น ละอองจากการปล่อยเป็นอากาศหรือน้ำเสียจากโรงงาน หรือการจัดเก็บน้ำเสียที่มีสารเคมี สารเคมีเหล่านี้อาจมีผลกระทบต่อระบบนิเวศและสิ่งมีชีวิต ซึ่งสามารถทำให้เกิดการเปลี่ยนแปลงที่ไม่พึงประสงค์ในสิ่งแวดล้อม ซึ่ง2อย่างนี้มีความเกี่ยวข้องกับ Environmental toxicology
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 20 |
จาก Engineered brain-targeted drug delivery systems ที่ใช้คืออะไร
|
5. ไม่มีข้อใดถูก |
|
Engineered brain-targeted drug delivery systems คือระบบการส่งยาที่ออกแบบมาเพื่อเป้าหมายการส่งยาเข้าสู่สมองในที่ที่ต้องการ โดยระบบนี้ใช้เทคโนโลยีและวัสดุที่เข้ากันได้กับระบบประสาทสมองเพื่อให้ยาสามารถเข้าถึงและทำงานในส่วนสำคัญของสมองได้
มีหลายวิธีในการพัฒนา engineered brain-targeted drug delivery systems ซึ่งรวมถึงการใช้งานตัวกำหนดยา (drug carriers) เช่น ลิโพโซม, ลิโปโซม, มิโคโรโนเลลส์ เป็นต้น ซึ่งสามารถรับยาและส่งยาเข้าสู่สมองได้อย่างแม่นยำ นอกจากนี้ยังมีเทคโนโลยีอื่น ๆ เช่น นาโนเทคโนโลยี การใช้กำลังไฟฟ้า เทคนิคส่งสัญญาณเสียง หรือสัญญาณแม่เหล็ก และวิธีการอื่น ๆ ที่มีประสิทธิภาพในการส่งยาสู่สมองเพื่อรักษาโรคหรือสภาวะที่เกี่ยวข้องกับสมองในลักษณะที่เป้าหมายได้เฉพาะ
|
Engineered brain-targeted drug delivery systems คือระบบการส่งยาที่ออกแบบมาเพื่อเป้าหมายการส่งยาเข้าสู่สมองในที่ที่ต้องการ โดยระบบนี้ใช้เทคโนโลยีและวัสดุที่เข้ากันได้กับระบบประสาทสมองเพื่อให้ยาสามารถเข้าถึงและทำงานในส่วนสำคัญของสมองได้
มีหลายวิธีในการพัฒนา engineered brain-targeted drug delivery systems ซึ่งรวมถึงการใช้งานตัวกำหนดยา (drug carriers) เช่น ลิโพโซม, ลิโปโซม, มิโคโรโนเลลส์ เป็นต้น ซึ่งสามารถรับยาและส่งยาเข้าสู่สมองได้อย่างแม่นยำ นอกจากนี้ยังมีเทคโนโลยีอื่น ๆ เช่น นาโนเทคโนโลยี การใช้กำลังไฟฟ้า เทคนิคส่งสัญญาณเสียง หรือสัญญาณแม่เหล็ก และวิธีการอื่น ๆ ที่มีประสิทธิภาพในการส่งยาสู่สมองเพื่อรักษาโรคหรือสภาวะที่เกี่ยวข้องกับสมองในลักษณะที่เป้าหมายได้เฉพาะ
|
7 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|