| 1 |

|
ข้อ 5. |
|
เมื่อลองเอาตัวเลขในตัวเลือกไปแทนค่าแล้วจะเห็นว่า ค่าที่มีความใกล้เคียงกับตัวแปรxที่สุด คือ 25/63 |
ตัวแปรสุ่มชนิดไม่ต่อเนื่องคือ ตัวแปรสุ่มที่มีค่าเป็นจำนวนเต็มบวกหรือศูนย์ |
10 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 2 |

|
ข้อ 2. |
|
เมื่อลองนำค่าP(X=x)มาบวกกันจะได้ค่าE=7ซึ่งจากโจทย์Xต้องมีค่าระหว่าง0ถึง2 มี3จำนวน ซึ่งP(X)ก็คือ2³=8ซึ่งเหลือค่าX(2)อีก2;เท่ากับ2/7 |
ตัวแปรสุ่มชนิดไม่ต่อเนื่องคือ ตัวแปรสุ่มที่มีค่าเป็นจำนวนเต็มบวกหรือศูนย์ |
10 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 3 |

|
ข้อ 5. |
|
หาความน่าจะเป็นจากตัวแปรสุ่มในโจทย์โดยหาจากตัวเลือก5ตัวเลือก |
ตัวแปรสุ่มชนิดไม่ต่อเนื่องคือ ตัวแปรสุ่มที่มีค่าเป็นจำนวนเต็มบวกหรือศูนย์ |
10 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 4 |

|
ข้อ 2. |
|
นำมาหาค่าเฉลี่ยคือนำ0+5+10+15+20แล้วหารด้วย5 ก็จะได้ค่าความแปรปรวนของตัวแปรสุ่ม ส่วนค่าคาดหมายเกิดจากการนำค่าทั้งหมดมาบวกกัน |
ตัวแปรสุ่มชนิดไม่ต่อเนื่องคือ ตัวแปรสุ่มที่มีค่าเป็นจำนวนเต็มบวกหรือศูนย์ |
10 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 5 |

|
ข้อ 4. |
|
นำ 0.343+0.784+0.973+1แล้วหารด้วย4ก็จะได้ค่าp |
การแจกแจงทวินามคือ การแจกแจงตัวแปรสุ่มที่ไม่ต่อเนื่องเกิดผลลัพธ์เพียง2อย่าง คือ สำเร็จกับผิดหวัง |
10 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 6 |

|
ข้อ 3. |
|
ตามทฤษฎีแล้ว กราฟของฟังก์ชันความหนาแน่นจะอยู่ได้แค่ควอรันต์ที่1และ3 เท่านั้น |
ฟังก์ชันความหนาแน่นของความน่าจะเป็นคือ ชุดของค่าที่เป็นไปได้ดำเนินการโดยตัวแปรสุ่ม |
10 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 7 |
|
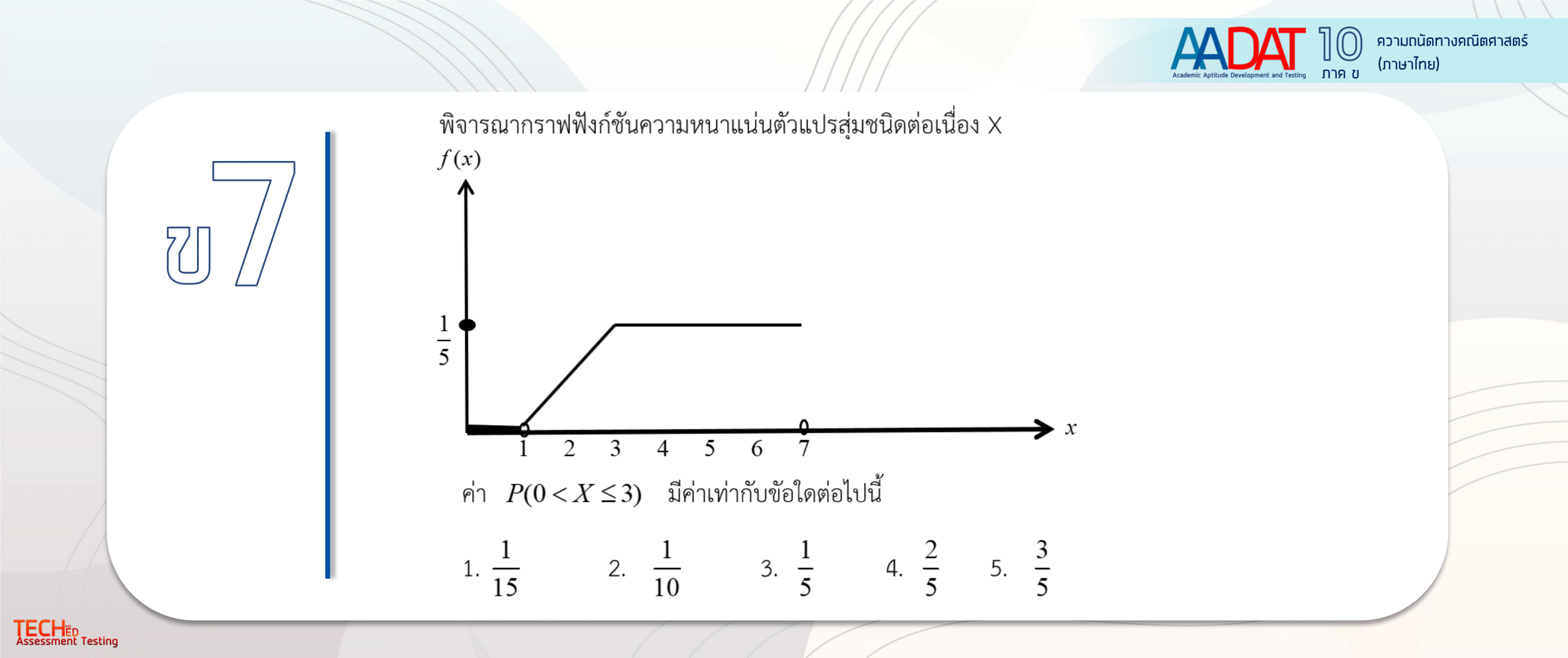
ข้อ 3. |
|
หาได้จากพื้นที่สามเหลี่ยมจุดx=1-3คือ1/2*2*1/5
2 เกิดจากการนำx=3-1=2 |
ฟังก์ชันความหนาแน่นของความน่าจะเป็นคือ ชุดของค่าที่เป็นไปได้ดำเนินการโดยตัวแปรสุ่ม |
10 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 8 |
|
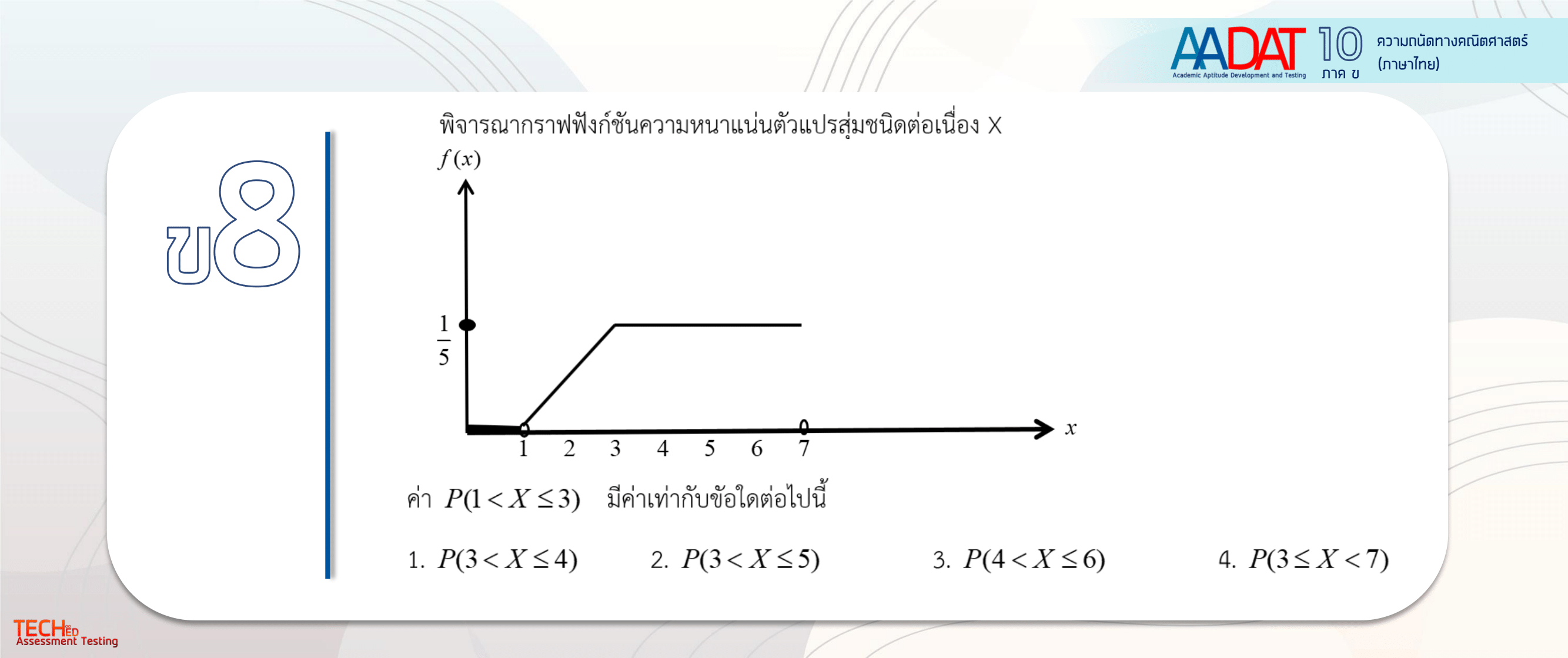
ข้อ 1. |
|
หาได้จากพื้นที่สี่เหลี่ยมคางหมูx=2ถึง3 คือ1/2*(1/3+1/5)*1 ซึ่งมีความใกล้เคียงกับตัวเลือกข้อที่1ที่สุด
ค่าความสูง 1 เกิดจากการนำx=3-2=1 |
ฟังก์ชันความหนาแน่นของความน่าจะเป็นคือ ชุดของค่าที่เป็นไปได้ดำเนินการโดยตัวแปรสุ่ม |
10 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 9 |

|
ข้อ 3. |
|
นำ0.5+0.625แล้วก็หารด้วย2 ก็จะได้0.2625 หรือประมาณ1/4 ซึ่งก็คือค่าความแปรปรวน |
u(มิว)คือ ค่าความแปรปรวน |
10 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|
| 10 |

|
ข้อ 5. |
|
ใช้สูตรส่วนเบี่ยงเบนมาตรฐาน=√(100-47.1)²แล้วหารด้วย100 |
ค่าส่วนเบี่ยงเบนมาตรฐานคือ การสัดกระจายแบบหนึ่ง สามารถนำไปใช้ในการหาความน่าจะเป็น ตัวแปรสุ่ม ประชากร หรือมัลติเซต |
10 |
-.50
-.25
+.25
เต็ม
0
-35%
+30%
+35%
|